Bootstrap
Bootstrapping of a Rates or Credit curve is the method of using a number of different term rates to get intermediate forward discount rates.

The concept comes from if you are putting on a pair of boots, to tighten the laces you need to start at the bottom and work your way up, tightening each level as you work up the boots. In the image shown you should start by tightening 9 and working backwards (up the boot) to 8, then 7 then 6... if you were to start at the highest point (1), when you pull on the laces at 2 it will loosen 1 and you need to start again.
In a similar way if you have the rates for 1, 2, 3, 4 and 5 years (from spot), to bootstrap the curve you start with the 1 year rate (1y), then you solve for the 1 year rate 1 year forward (1y1yf), when this is combined with the 1 year rate you should match the rate you have for 2 years.
Then you move onto the 1 year rate, 2 years forward (1y2yf), and by combining this with the 1y and 1y1yf you solve for the 3y rate
Simple Averages
A numerical example can be done with averages.
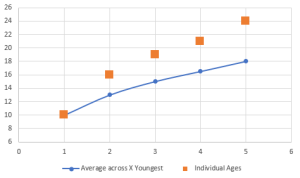
If you have a group of 5 people, the age of the youngest is 10 years, the average age of the two youngest is 13 years. The average age of the three youngest is 15 years, the average age of the 4 youngest is 16.5 years and the average age of all of them is 19 years.
What is the age of each person?
Using the letters A-E as the ages of the people, youngest to oldest these represent the Forward points on the Curve and the average can represent the term Rates.
Mathematically:
A = 10
(A+B) / 2 = 13 => B = 26 -10 = 16
(A + B + C) / 3 = 15 => C = 45 - 26 = 19
(A + B + C + D) / 4 = 16.5 => D = 66 - 45 = 21
(A + B + C + D + E) / 5 = 18 => E = 90 - 66 = 24
It seems trivial but it's obvious you have to start at the bottom and work up. The same can be applied to Bootstrapping of Credit curves and Rates curves where you may know the 1 3 5 7 and 10 year rates but need to work out from the 7 and 10 what the 3y7yf rate is since it's (almost) definitely going to be different from the 7 year or 10 year rates
Using Simple Interest Rate Swaps

Taking a bunch of very simple IRS we can boostrap a curve in Excel. The attached sheet will walk you through the process
If you solve for 0 PV on each interest rate swap you can get a solution as shown on the right.
A more advance method would be to have a real curve where each intermediate point is set and then a smooth function up to the next point, instead of the example used which is a stepwise function.